the five people you meet in heaven

As mentioned in the previous post, I had decided to try to read as many of the 100 books listed in Waterstones '25 year celebration' booksellers' choice.

The first one is: "the five people you meet in heaven" by Mitch Albom.

This was a very pleasant 'one-sitting' read - nicely written, but with no great or profound insights. The ideas are of the 'every ending is also a beginning', 'all our lives are connected' and 'the only wasted time is the time thinking we are alone' variety.

Things I liked: The 'Whrrsssssh' of the waves breaking on the beach; that he (i.e. Eddie, the central character of the book) loved his wife; and that he did not hve children of his own.

Things to keep you reading: Did he save the child from the falling "Freddy's Free Fall" (a funfair ride at Ruby's Pier)?; What happened with Marguerite (his first true love)?; and Was there a child in the burning building?

In my opinion, the main weakness of the book was that it centred only on 'life-and-death' issues, while, in reality, our lives are shaped as strongly by smaller tragedies and joys. Perhaps it was also slightly forced that so many of the events occurred on Eddie's birthdays.

Would definitely not be on my personal top 100 of all time, but can see why it made it onto the Waterstones list.

25 Years in Books

At the moment, Waterstones are celebrating their 25 th year and are calling readers to vote for the favourite out of 100 books published in the last 25 years.

Of these 100 books, I had only read 23! And 8 of those were books that I really did not like all that much.

Anyway. I voted for my favourite from the list (Jonathan Strange and Mr Norrell by Susanna Clarke) and decided that I would try to read as many of the books on the list as possible!

While I am sure that most of the books on this list are excellent, I was surprised that there were NO books by:
PD James,
Patricia Cornwell,
Kathy Reichs,
Steven King,
Jostein Gaarder,
Alexander McCall Smith, or
Jacqueline Wilson

My favourite book written in the last 25 years: 'How to be good' by Nick Hornby was also not there and neither were 'We need to talk about Kevin' (Lionel Shriver) and 'Death and the penguin' (Andrey Kurkov).

Armed, with the list, I went to my local library, and I made the following observation:
Most of the books in the library were not on that list. I hypothesise two reasons for this:
(1) Even though books are being published at an ever increasing rate, most of the books out there were written more than 25 years ago.
(2) People borrow newer, good books preferentially over old favourites.

Coffee Breaks

For those of you who at times enjoy a bit of mindless internet sport, why not try:
Google Image Labeler.

The chemists among you might also enjoy perusing The Chem Blog. It is obviously a bit more intellectual than the Love Calculator and Image Labeler, but still a good diversion.

True Love

I have just entered Alain and my name into the Love Calculator:

I have entered hordes of name combinations and have not been able to beat that, so it must be true love!

Scaramantic discovery

Alain and I went to South Africa for Christmas last year. As usual, before we left, I returned all the books, DVDs etc that I had borrowed from people as I am always paranoid that the plane will explode and... well, I don't really want to die not having returned other peoples' property to them.

I mentioned this to one of my colleagues who told me that I was definitely not Italian to which I proudly replied: 'I am not in the slightest bit scaramantic!'*

To my chagrin, I have since discovered that I do have (at least) one scaramantic quirk. While on holiday, I lost a rather expensive work-related item which had to be replaced on my return. My boss emailed me to tell me that I should be careful not to lose it. When I read this email I had the overwhelming (and obviously irrational) feeling that her telling me this had increased the probability that the replacement would be lost in the near future.

........................................................................
*The reply to this statement was quite amusing, but perhaps not suitable for a mixed audience. I am dying to tell you - please email me and I will fill you in.

10 January 1998

This post is to remember Alain and my wedding day, 10 January 1998. The wedding took place in Durban, South Africa.

The photographer really liked the little flower-girl and there were literally hundreds of photos of her and only about 10 of me! She is all grown up now and still very beautiful.

To give you an idea of how long ago everything was: the first film we went to see as a married couple (on our honeymoon) was 'Titanic'. There isn't really much else to say except that we are still happily married.

Happy New Year!

It is 2007! Can you believe that seven years have elapsed since we were all panicking about the millenium bug?

I would like to take this opportunity to say 'Happy New Year!' and share a festive philosophical musing.

Karl Marx famously stated that "Religion is the opiate of the masses" and, more recently, Bill Watterson drew a television with a thought bubble saying "Karl Marx ain't seen nothing yet".

If the destiny of the masses is to relinquish the power that they have over their minds and lives, it is sad that the trend of western society is to choose television over religion. Religion, with all its faults, at least has the advantage of calling people to high ideals and a structured community. Has the overall result of progress merely been the transfer of dependance to a lesser god?

Sudoku (Part IV)

For me, one of the most attractive qualities of the Sudoku as a puzzle is that there is a wide range of difficulty levels. This means that the puzzle is accessible to people with very different natural logical abilities, and as you improve, you can do slightly more challenging ones.

Usually in newspapers these are labeled in some way, e.g. mild, moderate, difficult and diabolical. But yet the puzzles look more or less the same. The difficulty level does not seem to be directly related to the number of clues or the arrangement of these in the grid, so unless you know the rating, you cannot tell whether the solver is a novice or an expert.

I am the only person that I ever see on the train who is trying to build their own Sudoku, so this is not a common pursuit, though I think that you might find it quite rewarding once you get started. My observations and ideas are still in the process of evolving, so I would like to re-iterate that this blog is to share where I have got so far and that it would be nice if you posted comments with your own observations and Sudoku-creations. I envision that my commentary will span 3 more blog entries after this one.

To make a Sudoku problem, we need to have a 'true' Sudoku matrix. For advice on how to prepare these click here to start at the beginning. My overall approach is to use the Sudoku matrix to add clues to a blank grid (these will be formated as lower-case letters), solve as far as possible (letters added in the solution process will be formated as capital letters), and repeat until the problem is completely solved.

The first observation that I would like to make regards ensuring that clue-matrix will result in an unique solution. Lets have a look at the matrix that we prepared in Sudoku (Part III):

You will notice that the identities of the four shaded boxes are only dependant on each other. The b's and e's can be interchanged without affecting the rest of the matrix.

In setting the clues for this puzzle it is necessary, therefore, to include at least one of those four letters as it is not possible to give unambiguous, indirect clues that will enable the solver to decide which way round these b's and e's should go.

The first thing that I do is to try to identify all of the interchangable foursomes. These are the ones that I can see on this matrix:

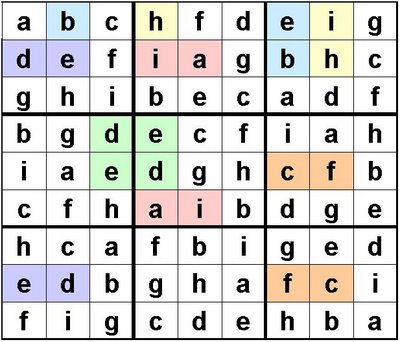
Our clue-matrix must therefore contain one letter from each of these interchangable-foursomes.