Sudoku (Part IV)

For me, one of the most attractive qualities of the Sudoku as a puzzle is that there is a wide range of difficulty levels. This means that the puzzle is accessible to people with very different natural logical abilities, and as you improve, you can do slightly more challenging ones.

Usually in newspapers these are labeled in some way, e.g. mild, moderate, difficult and diabolical. But yet the puzzles look more or less the same. The difficulty level does not seem to be directly related to the number of clues or the arrangement of these in the grid, so unless you know the rating, you cannot tell whether the solver is a novice or an expert.

I am the only person that I ever see on the train who is trying to build their own Sudoku, so this is not a common pursuit, though I think that you might find it quite rewarding once you get started. My observations and ideas are still in the process of evolving, so I would like to re-iterate that this blog is to share where I have got so far and that it would be nice if you posted comments with your own observations and Sudoku-creations. I envision that my commentary will span 3 more blog entries after this one.

To make a Sudoku problem, we need to have a 'true' Sudoku matrix. For advice on how to prepare these click here to start at the beginning. My overall approach is to use the Sudoku matrix to add clues to a blank grid (these will be formated as lower-case letters), solve as far as possible (letters added in the solution process will be formated as capital letters), and repeat until the problem is completely solved.

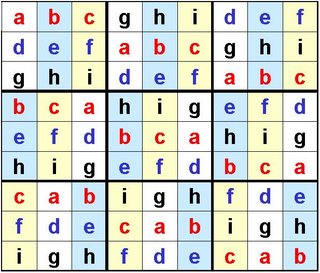
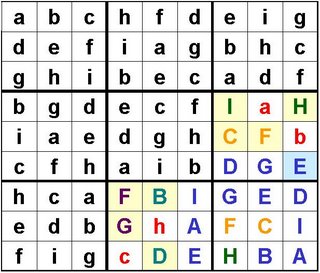
The first observation that I would like to make regards ensuring that clue-matrix will result in an unique solution. Lets have a look at the matrix that we prepared in Sudoku (Part III):

You will notice that the identities of the four shaded boxes are only dependant on each other. The b's and e's can be interchanged without affecting the rest of the matrix.

In setting the clues for this puzzle it is necessary, therefore, to include at least one of those four letters as it is not possible to give unambiguous, indirect clues that will enable the solver to decide which way round these b's and e's should go.

The first thing that I do is to try to identify all of the interchangable foursomes. These are the ones that I can see on this matrix:

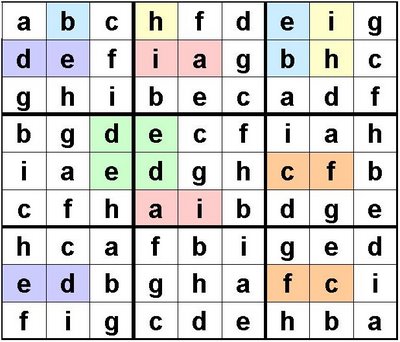
Our clue-matrix must therefore contain one letter from each of these interchangable-foursomes.

Sudoku (Part III) The last example matrix

To start from the beginning, go to: Sudoku (Part 1)

The last example of a matrix preparation is one where the letters are arranged more-or-less randomly. When doing this, I would advise stopping for a moment at a point where you have 6 filled blocks arranged, for example, like so:

At this point, you should be paranoid about checking that the blocks so far are 'true'.

The next step, is to solve the Sudoku as far as possible to see what positions are already forced (i.e. where only one letter will give true matrix), and which can only be one of two letters.

Proceeding from this point, can involve a bit of trial and error, so don't get too discouraged if you find yourself with a 'false' solution, for example, the first choice of the positions of h and i, turned out to be a mistake:

Solving the Sudoku after choosing H and I in the respective yellow shaded slots, results in the arrangement of letters shown in green capitals. You will notice in the figure above, that now there is no correct place to insert a B in the row shaded in blue. The positions of H and I were incorrect and must be reversed.

Keep repeating this process with pairs of letters until you have solved the puzzle.

Sudoku (Part II) Adding complexity to the matrix

To start from the beginning, go to: Sudoku (Part 1)

The next example matrix starts by arranging the letters in the top three blocks in a slightly more random fashion:

Instead of just copying the mini-columns to the left or right to form the lower and middle left two blocks, we can muddle the letters within the mini-columns:

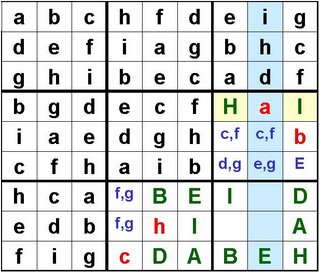
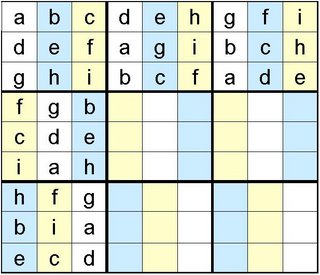You will notice now, that it might be quite easy to get things wrong when filling out the last four blocks.

You can now play around with building matrices that are based on patterns. You will find that it is much easier to obtain a 'true' matrix quickly if use patterns. If however, you get bored with doing it like this, and start wanting to arrange the matrix more-or-less randomly, you might want to go to the next post in this Sudoku series.

Sudoku (Part 1)

A few weeks ago, I made some observations about things that people do on the train. If you would normally do something like a Sudoku puzzle, then I can suggest another intellectual pursuit that you can do if you only have a pencil and the back of an envelope (or that paperwork that you don't feel like doing any more).

You can try to build your own Sudoku.

For the next few posts I am going show you an approach to doing just this. These will not be definitive 'how to' tutorials - just a few things that you can play with in order to get going. Perhaps if you have some insights, or ideas, you could share them by posting a comment.

In this first entry, we will look at the matrix, a 9x9 grid.

In this post and in all the later ones, the letters a-g will be used instead of numbers. The reason for this is that this makes notation easier for me, and will have the bonus that when you set the problems for other people, you could set a, for example, to be any of the numbers from 1-9. The starting grid will always be the left-top one, and the letters will always be arranged as shown:

(This is just my preference - playing around with different starting positions, could probably be a whole hour of fun on its own!)

The most facile matrix is made simply by moving entire mini-rows...

... and mini-columns.

Remembrance Day

Today I would like to remember my grandfather who fought in the Second World War. He was one of many people to be taken as a prisoner of war after the Allies' defeat in Tobruk.

He enjoyed telling people that as a prisoner of war his job was to sort the German outgoing mail, and that he put the envelopes in the wrong bags! Apparently the German's were amused rather than angry about this when they found out. I wonder how true that was?!

The other related thing that I remember is that whenever any of us complained about being overweight, he would say: 'Just eat less. There were no fat prisoners of war.'

Finding prime factors

This is an entry for those of you who would like to have a quick mental-calculation method to see whether one number is a factor of another number, or to find out whether your number is prime. [The size of the number that you could investigate will depend on your confidence in your short term memory.]

So, if we take the number a = 493 as an example.
We can see that it is not divisible by 2 (the right-hand most digit is an odd number), 3 (the digits do not add up to a multiple of 3) or 5 (the right-hand most digit is neither 5 nor 0).

Apart from actually doing the sums, is there a way of finding out whether 493 is divisible by other prime numbers like 7, 11, 13 and 17? While in this case it is easy to see that 493 is not divisible by 7, I would still like to use 'Is 7 a factor of 493?' as an example of a method to find prime factors for a given number.

In order to understand this method, let's ask the following question: Why did I say that it is easy to see that 493 is divisible by 7?

The reason is that we know that 490 is divisble by 7 and that 3 is not divisible by 7, therefore 490 + 3 cannot be divisible by 7. In other words, if 493 minus a multiple of seven is not divisible by seven, then 493 is not divisible by 7.

Another multiple of 7 is 21.

21 is interesting in that 21*3 = 63. i.e. 21 multiplied by the last digit of our number (493) gives a number that also ends in 3.

493 - 63 = 430. Now we know that 42 is multiple of 7, therefore 43 is not. It follows then that 430 is not divisible by 7, and from our previous reasoning, this means that 493 is also not divisible by 7. A useful observation is that we can just ask if (49 - 6) [i.e. (49 - 2*3)] is divisible by 7.

The first step in our method is thus to find a multiple of our divisor that ends in 1.

1. Multiply the divisor by a number such that the product will have 1 as its right-hand most digit. In this case 7 * 3 = 21.

2. Subtract 1 from this product and divide by 10 to give y. In this case y = (21-1)/10 = 2. [i.e. Chop off the one!]

3. Multiply the right-hand most digit by y to give r (3y = 6 = r).

4. Chop the right-hand most digit off the original number a to give b (493 -> 49).

5. Substract r from b to give c (c = 49-6 = 43 ).

6. Ask the question: Is c divible by 7? If yes, then a is divisible by 7. If no, then a is not divible by 7. If uncertain, repeat steps 3-6 using c instead of a. If c = 0 then a is divisible by 7. In this case, 43 is not divisible by 7, therefore 493 is not divisible by 7.

What about 11?
We don't need to multiple 11 by anything to get a product ending in 1. We just use '1'.
49-3 = 46. 46 is not divisible by 11, therefore neither is 493.

What about 13?
1. 13*7 = 91
5. 49 - 9*3 = 22.
6. 22 is not divisible by 13, therefore neither is 493.

What about 17?
1. 17*3 = 51
5. 49 - 5*3 = 34
6. 34 is divible by 17, therefore so is 493.

What about 19?
1. 19*9 = 171
5. 49 - 17*3 = 49 - 51 = 2
6. 2 is not divisible by 19, therefore neither is 493.

What about 23?
1. 23*7 = 161
5. 49 - 16*3 = 1
6. 493 is not divisible by 23.

What about 29?
1. 29*9 = 261
5. 49 - 26*3 = -29.
6. 493 is divisible by 29.